The Open University
Introduction
Actual or nominal rates of interest are sometimes contrasted with real interest rates which take into account inflation. Estimates of real rates of interest have usually been made in the context of the construction of models which explain interactions in money markets in terms of expectations about future interest rates. This note describes a method of measuring real interest rates empirically and historically.
The method
The method was developed to help measure the impact of inflation on new town development corporations. The corporations borrowed money for a fixed period of fifty years at fixed rates of interest. Rates of interest varied from 3% in 1947 at the beginning of the programme up to 18% charged in the mid 1970s. Typically the annual borrowings of an individual corporation increased every year for a period of five to ten years as construction got under way. Then after a peak there were continued annual borrowings for up to thirty or years at a lower level as the new town continued to grow.The period of new town construction in Britain was one of continued inflation. After the first decade of the life of the corporation most of the advances on which the corporation was paying interest were made at a time when the price level was substantially lower. The real rate of interest, taking into account inflation, is lower than the rate of interest actually paid.
The real rate of interest does not take into the full impact of inflation on the finances of the development corporations, but is limited to indicating the impact of inflation on the General Revenue or current account. Inflation also had an impact on capital account as expressed in the Balance Sheet. This note does not attempt any estimation of the influence of inflation on capital account because of the practical and conceptual problems involved, but does later discuss the influence of inflation on the relationship between the pictures given by the current and capital accounts.
The calculation of the real rate for any particular year is based upon all advances made earlier than that year, the rate of interest which was fixed at that time an advance was made, and the inflation which has taken place since the advance was made:
Let Ln= advances made in year n, and Rn= the rate of interest charged for advances made in year n (which are fixed for the life of the loan). Then It, the nominal interest paid in year t for a series of advances beginning in year 1, is given by:
It = *Ln*Rn (from n=1 to n=t).
Then ARt, the average nominal rate of interest paid in year t, for a series of advances made in year 1 or in later years, is given by:
ARt = *Ln*Rn/*Ln (from n=1 to n=t)
Let Pn= the price level in year n. Then the basic assumption in the estimation of real interest rates is that RRtm, the real interest rate paid in year t for an advance given in year m, is given by:
RRtm = Rm*Pm/Pt
This assumption defines the real rate of interest as something measured historically and not something which can be measured at the time an advance is made. The definition implies that the real rate of interest continues to fall for as long as inflation continues (and that the real rate would increase if there were a fall in the general price level). With hyperinflation or inflation over a very long period of time the real rate may approach zero, but it cannot be negative as it can be in some models which have used the concept of real rates of interest in association with expectations about future levels of inflation.
It follows from this definition that ARRt, the average real rate of interest paid in year t for a series of advances, is given by:
ARRt = (*Ln*Rn*Pn/Pt)/*Ln (from n=1 to n=t)
The method of calculation of real interest rates actually used is slightly different,. The accounts of the development corporations give total interest payments made each year, ie It=*Ln*Rn (from n=1 to n=t). These figures were used in as the preferred source for interest payments because no details are given in the annual reports of the method of calculation used for the calculation of the "average" rate of interest paid which are also included in most of the annual reports.
Another factor is that the accounts of the development corporations include figures for the sum of advances, ie *Ln, as the sum at the end of the financial year. In the formulae given above it has been implicit that the sum of advances refers in some way to the year as a whole. In the calculations made the sum of advances has been measured as the mean of advances made at the beginning and end of the year. The average nominal rate of interest in year t can then be written as:
ARt = 200*It/(*Lt + *Lt-1)
The method used for the calculation of the real rates of interest was designed to take advantage of the relative addressing facilities of a spreadsheet. RI2, the real level of interest payments made in year 2, for example, was calculated as the sum of interest paid for advances made in year 2 plus the interest paid in year 1 deflated by the increase in the price level in year 2 relative to year 1:
RI2 = I2 - I1(1-P1/P2)
Generalising this, and using the relative addressing facilities of the spreadsheet, the level of real interest for all years were calculated as the sum of interest paid for advances made in the current year (measured in terms of It-It-1) plus the real interest paid in the previous year (ie RIt-1) deflated by the increase in the price level since the previous year:
RIt = It - It-1 + RIt-1*Pt-1/Pt
The Retail Price Index was used as a measure of the price level. The calculations were made using the Excel 5 spreadsheet. Columns A to D gave the input for the calculations. Column A was used for the financial years. Column B for advances made (Ln), column C for the interest payments made (In), and column D for Retail Price Index expressed with a common base year.
Columns E and F were used for calculation of the nominal and real rates of interest. The expression copied for the average nominal rates given in column E was ARt = 200*Ct/(Lt+Lt-1) - and the figures obtained by this method approximated to the figures given in many of the annual accounts for the average interest rate paid. Column F gives the average real rate of interest. The cell for year 1 for column F was entered manually as ARR1=F1=C1. The expression for the average real rate of interest copied for year 2 to year t is:
ARRt = 200*(Ct - Ct-1 + Ft-1*Dt-1/Dt)/(Bt+Bt-1)
Results for Harlow and Milton Keynes
Some practical results using this calculation are illustrated in the Chart which shows the rate of inflation as measured by year to year changes in the Retail Price Index and both real and nominal rates of interest paid by Harlow and Milton Keynes Development Corporations. Milton Keynes was designated twenty years later than Harlow and faced a very different economic environment in terms of higher levels of both interest rates and inflation. The estimation of real rates of interest makes it possible to make direct comparisons between the impact of interest payments on the two corporations.
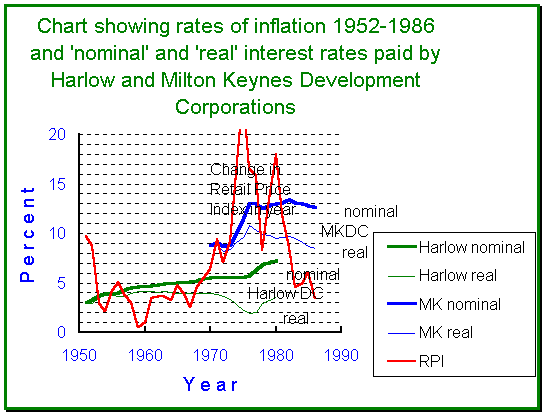At the end of its main nineteen year development period in 1986 Milton Keynes Development Corporation was paying an average rate of interest of 12.5%. But the real rate is estimated at 8.5%. The difference of 4% is a measure of the extent to which inflation reduced the real impact of Milton Keynes interest payments. At the end of nineteen years of Harlow�s development in 1966 the Corporation was paying an average rate of interest of 4.9%. But the real rate was 3.9%. Harlow at that stage benefited by inflation by only 1% - a quarter of the reduction of Milton Keynes.
Milton Keynes could be said to have gained more from inflation than Harlow, but this gain did relatively little to reduce the impact of the higher interest rates which Milton Keynes had to pay. The nominal interest rate of 12.5% paid by Milton Keynes at the end of its development stage in 1986 was a little more than two and a half times the 4.9% paid by Harlow in its nineteenth year. But the difference in real terms was not very much smaller. The real rate of interest of 8.5% paid by Milton Keynes was a little more that twice the 3.9% paid by Harlow.
The main difference in the impact of inflation on the financial situation of the two development corporations lies in the length of the development periods. Harlow Development Corporation had a longer life than Milton Keynes and continued to benefit from inflation for another fifteen years. Harlow had time to demonstrate profitability, and by the 1970s had begun to cumulate substantial financial surpluses. After 1974 Harlow was able to finance capital expenditures from its own resources and did not need to borrow money. The effect of rapid inflation in the 1970s was to reduce the real rate of interest paid by Harlow Development Corporation to less than 2% by 1976.
The reasons why both the real and nominal rates of interest paid by Harlow increased after 1976 provide an interesting vignette of the financial relations between central government and the development corporations. By the 1970s Harlow Development Corporation was able not only to finance its own investment but also lend to money. In the early 70s Harlow was paying 6% on the money it had borrowed from the Treasury but was earning something in the range of 10-15% in interest on the money it had on loan to other bodies. Harlow Development Corporation actually earned 2.2 millions in interest on its loans in 1976. It appears that the Treasury was not happy to see Harlow Development Corporation develop as a semi-autonomous lending institution, and the government appropriated 9m surplus from the Corporation in 1976. The nominal and real rates of interest paid by Harlow Development Corporation rose after 1976 because the Harlow Development Corporation was obliged to borrow more money at the then prevailing interest rates of 10% or much more.
At the end of its life in 1980 the real rate of interest paid by Harlow Development Corporation was a little over 3% as compared with the nominal rate of a little over 7%. Inflation had by the end of the life of Harlow Development Corporation reduced the interest real burden by 4%.
The influence of inflation on interest payments on the financial performance of the corporations is indirect rather than direct. Inflation does not influence the amount of interest actually paid. The concept of real interest rates as defined here implicitly assumes that money borrowed is invested in assets whose value increases with inflation. Assets belong to the capital account and are recorded in the corporations Balance Sheets at historic cost. But rent income derived from these assets is classified to the General Revenue Account where it is set against interest payments. The rate of return on assets is a measure of financial performance which is independent of interest rates paid by the corporation but is expressed in the same units as the rate of interest, and is a measure which will increase with inflation if the development corporation increases its levels of rents in accordance with the general level of prices.
The rate of return on the assets transferred to the Commission for New Towns by Harlow Development Corporation in 1980 at the end of its life was 12% - as compared with the nominal rate of interest paid of 7%. But the real rate of interest was only 3%. It seems reasonable to suggest that 4% of this 12% should be regarded as gain solely attributable to inflation. The other 8% is an indicator of the rate of return at that stage on Harlow's planning activities. The qualification "at that stage" is appropriate because it can be expected that rent income will usually lag inflation. The crucial component of the development corporations income comes from industrial and commercial property let on leases which may be subject to review only every five years or longer.
At the end of its development stage in 1986 the rate of return on capital expenditure by Milton Keynes Development Corporation was only 2%. The difference of 4% in that year between the nominal and real rates of interest paid suggests that the rate of return of 2% can be wholly attributable to inflation, and that at that stage of development, the benefits from the creation of new urban values in Milton Keynes had not begun to manifest themselves in levels of rent. In the case of Milton Keynes the value of the assets created became manifest only when they were revalued or sold in 1987 or later years. Concluding remarks The estimation of real interest rates seems particularly useful in the context of new town development because of the long period over which expenditures are made and over which financial performance might be evaluated. But the method of measurement described could be applied to the investigate the influence of inflation on any organisation which finances its investment from fixed interest loans. The method of calculation is of interest in demonstrating the extraordinary usefulness of the relative addressing facility of the spreadsheet.
No hay comentarios:
Publicar un comentario